Bitcoin, Metcalfe and Lindy – Bitcoin USD (Cryptocurrency: BTC-USD)

introduction

Some of you may have read my review of the Cryptolab capital's NVM report. If you have it, then you will know that there are three ways in which Metcalfe's law has been applied to cryptocurrency, in particular Bitcoin (BTC-USD) (OTCQX: GBTC) (COIN).

An important thing to note is that Metcalfe's law has already been adapted from its original form by Cryptolab Capital and others.

Image source: Cryptolab Capital

Today I will talk about my approach to this concept and why I think we need a new approach when it comes to Bitcoin.

The problem

There are two main problems that I saw insinuated in the calculations of Metcalfe's law to determine the value of Bitcoin's network. Are the following:

• We do not know how many Bitcoin users there are. The use of the number of "portfolios" is incorrect, because the number of portfolios must be added per platform. For example, the portfolio number you see on blockchain.com is just the number of portfolios created on the blockchain.com website, not all portfolios exist.
• Some users are inactive and some users are very active. It would be incorrect to treat them all the same way as regards their importance for the network.

So, what can you do?

My solution

From the point of view of Bitcoin, there is only one source of activity. This source is a Bitcoin address that contains an unspent output (a part of the UTXO set). That is to say, a Bitcoin address with some Bitcoins in it.

The most important event, the main function of Bitcoin is to be able to send a transaction. Only addresses with some Bitcoins can send a transaction (except for a coin-based transaction, which is when a miner receives the reward by block, this is when the new Bitcoin comes into play).

So, I think we can say that the total value of the network should be related to both the number of participants and the level of activity of those participants.

The next question you're probably thinking is, "Can we determine these things?" Fortunately, the answer is yes.

The number of unique addresses in use and the number of daily transactions confirmed on the chain are very close to us.

Test of the theory

To test this theory, I want to try a different approach. I remember a statistical lesson I took years ago. The professor told the class that before doing something extravagant, we should simply create a scatter plot and look at the data. Doing this gives you an idea of ​​what could happen. Only then would we actually "do something" with the data, to try and confirm our suspicions.

We start doing this. Without any processing, I present the number of daily transactions and the Bitcoin price.

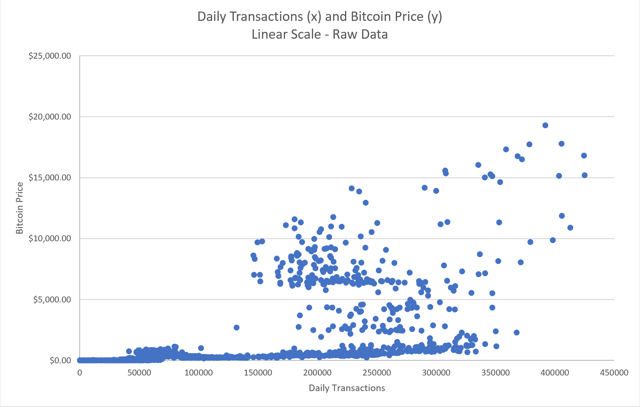Source: blockchain.com and graphics of the author

Hmm, what do you think? I'm not super convinced here. But, I seem to remember that with Bitcoin, we must think in the log scale. So, we take the log 10 basis of the transactions, and we do the same for the price, and look at this data again.

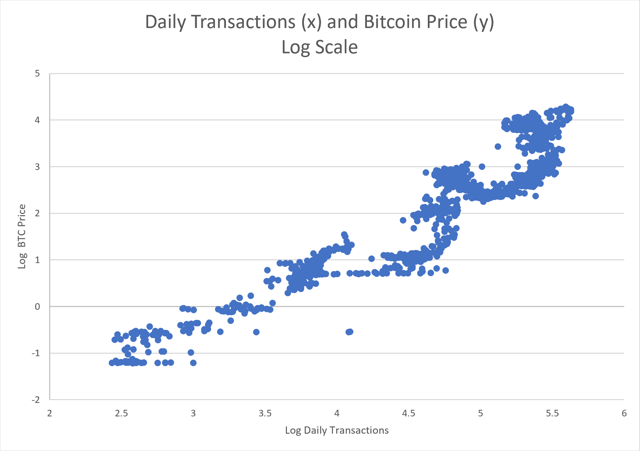Source: blockchain.com and graphics of the author

Well, look at this. It looks like a positive linear log-scale relationship if I've ever seen one.

Unique addresses

We check the number of unique addresses in the same way.

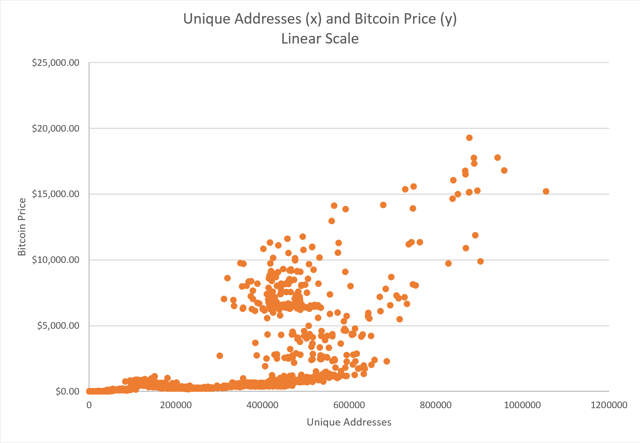Source: blockchain.com and graphics of the author

I think I see a relationship here, facing up and to the right. But is there any way to visualize these data that could improve our intuition?

Source: YouTube

Oh yes, register!

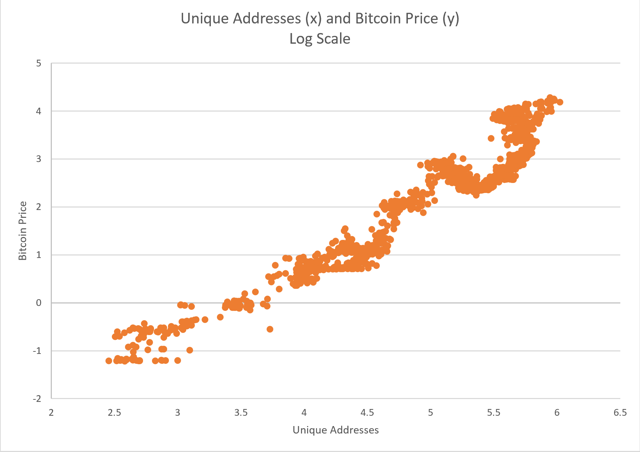Source: blockchain.com and graphics of the author

Jumpin & Jeochhaphat! Something is happening here.

Now some of you are thinking, "Yes, I know Hans, I've read all your articles, what's new for me?"

The V2.0 law of Metcalfe in 3D

I worked with a new graphics library called plotly.js. It was a great help. I started thinking, and if we could see all of this data at the same time?

I took the price of Bitcoin, the number of unique addresses and the number of daily transactions all in the same chart (log scale of course). So, I made it in 3D. This was the result.

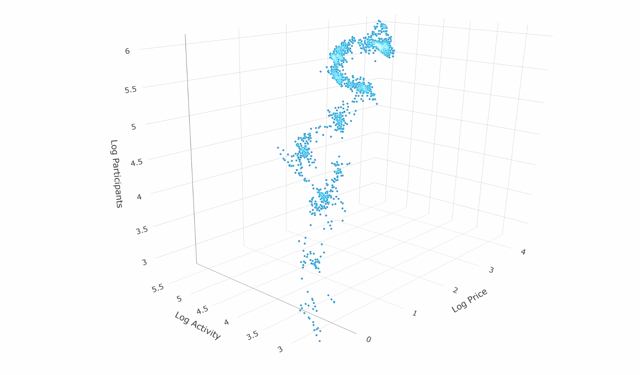Source: blockchain.com and new author graphics

Unfortunately, looking for Alpha does not like making GIFs in an article, so you'll have to do it click here to see this in live action. Please take a moment to watch the GIF 10 seconds before continuing with the article.

What the hell am I watching?

What you are looking at here is very dense with information. Unpack this one.

1. The "point of origin" is the point at which the registration price, the register activity and the register participants are at a minimum. If you are looking at the image above, that is the area closest to the blue dots in the center of the graph, near the bottom.
2. A point near the origin would be a point where the number of unique addresses was low, the daily transactions were low and the price was low.
3. If you imagine this as if you were inside a big cube, with the point of origin at an angle, the opposite point is where the prices are high, the unique addresses are high and the daily transactions are high.
4. As you can see, the points form a kind of spiral from the point of origin to the opposite corner of the cube. This indicates that when X increases, also Y and Z increase.
5. In other words, X, Y and Z move together.

If the result of this plot had been a perfectly straight line, going from one corner to another, we would have a model without variance. Unfortunately, this rarely happens in nature.

If we had a zero variance model, we could predict the exact Bitcoin price if we had the number of daily transactions and the number of unique addresses. But we do not have it. So, where does it leave us?

Where do we go from here?

The fact that we do not have a perfect model is both a blessing and a curse. On the one hand, we can not be too sure what to expect. But, on the other hand, this model puts us ahead of the curve as Bitcoin is so new. Very few people have a point of reference on everything based on data. Many people are simply abandoning the opinions of others.

You have to think about the price of Bitcoin at a given moment as existing in a probability field, or a probability cloud. The center of this cloud is the expected value. The actual price of Bitcoin is a point in the cloud. It is technically possible that the price of Bitcoin is everywhere, but it is more likely to find it closer to the center of the cloud.

Of course, we know from experience that it tends to bounce. These are the Bitcoin bubbles! The price type of Bitcoin orbits around the central point (which in turn is moving), sometimes it is too low and sometimes it is too high.

You can create a model in which we simply take the number of daily transactions and the number of unique addresses, and then use them to create a price forecast. The results are not bad, even if the data are not normally distributed.

Is there an even better way?

Let's talk about the Lindy effect for a moment. This idea was first suggested by Goldman in 1964, but was re-mentioned by Mandelbrot and finally by Nicholas Nassim Taleb in 2007, and again in 2012.

If a book has been printed for forty years, I can expect it to be printed for another forty years. But, and this is the main difference, if it survives another decade, then it is expected to be printed for another fifty years. This simply tells you why the things that have existed for a long time do not "age" like people, but "age" on the contrary. Every year that passes without extinction doubles the additional life expectancy. This is an indicator of a certain robustness. The sturdiness of an object is proportional to its life! ^[5]

What would happen if we included an element that reflected the passage of time? I tried this, and I was pleasantly surprised by the results. By adding a third input, the total of all confirmed transactions, the predictive value skips and the standard error drops. I attribute this improvement mainly to these two factors:

• The number of unique addresses and total transactions are not perfectly independent from each other. Because they tend to move together, part of the model's power is limited using both inputs.
• The Lindy effect is having an impact. The longer Bitcoin survives, the more people feel at ease. Whenever a bubble breaks out, but afterwards the Bitcoin recovers (which has already happened many times), more people take note.

Return to the Z-Signal Bitcoin

It only happens that the Bitcoin Z-Signal is the model I described above. The Z-Signal (and its cousin, the Z-complex) are approaches to derive the value of Bitcoin from the network, weighted by time in the hypothesis that the longest Bitcoin survives, the more likely it is to persist.

The Z complex of Bitcoin

Let's take a look at the latest chart of Bitcoin's Z complex. But, before doing so, I want you to think of the Z scores down as an expression of the current distance of the Bitcoin price from where it was expected (because that's what it actually is, in terms of the number of standard deviations).

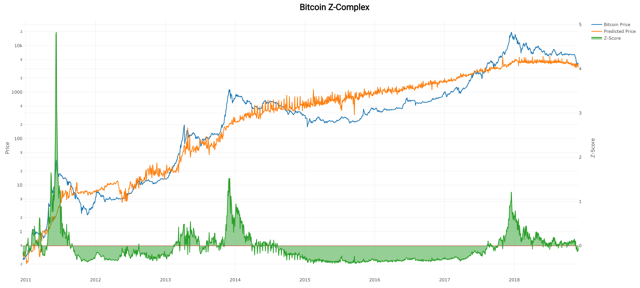Source: blockchain.com and new author graphics

Does this chart have a little more sense now?

Also, remember what Hal Finney said:

Every day that passes and Bitcoin has not collapsed due to legal or technical problems, this brings new information to the market. Increases the probability of final success of Bitcoin and justifies a higher price. – Hal Finney, June 4, 2011 – Discussion forum on Bitcoin

Conclusion

I argue that in order to correctly apply the Metcalfe Law to Bitcoin, we must consider the number of participants and the amount of activity that is occurring. After all, a million people sitting down to do nothing is not exactly a healthy network, and the same can be said of a person who sends a million transactions a day. Only when many people send many transactions do we have a healthy network.

In addition, adding the total number of transactions never confirmed to the mix, we can produce an even more powerful metric, which I call the Bitcoin Z-Signal (the Z-Complex is the Z-Signal with the expected price included).

This point is best illustrated by the following table:

	Unique addresses	Daily transactions	Z-Signal
R ^ 2	, 909.572602 millions	, 925,638558 millions	, 942.293654 millions
Standard error	, 378.436335 millions	, 476.216125 millions	, 317.717411 millions

Source: blockchain.com and models of the author

The Z signal is more predictive and has a lower standard error than the Metcalfe inputs alone. So, I argue that this approach is a way to extend and improve previous models that have come before.

This article was first published in Crypto Blue Chips.

Revelation: I am / we are long BTC-USD.

I wrote this article alone, and expresses my opinions. I'm not getting any compensation for this (other than Seeking Alpha). I have no business relationship with any company whose actions are mentioned in this article.

Additional disclosure: The articles now require a "bullish", "bearish" or "neutral" rating. However, they do not ask for a period of time. My official position is that, in the long run, I am very bullish, but in the short term I think the price could fall further. Therefore, short-term bearish, long-term bullish.