 [ad_1]
[ad_1]
introduction
One of the best techniques I know to sniff the relationships between data sets is simply to put it on a scatter plot. I talked about it in my recent article, Bitcoin, Metcalfe and Lindy (BTC-USD) (OTCQX: GBTC) (COIN).
If you did this, and there seems to be some sort of association (the zero correlation would be 0, the perfect positive associations occur at +1, the perfect negative associations are represented as -1), you may want to look for an equation to define this relationship.
An easy way to do this is to use linear regression. But this approach comes with its own limits and restrictions. For one, linear regression is supposed to be used on normal data sets. This means that all those trend lines you drew on a monthly sales chart were actually high crimes for the academic world.
However, I argue that the use of regression in this way has its merits for a number of reasons.
- Even if it does not produce the perfect solution, often the output is far ahead of the existing models and brings us closer to the truth.
- Sometimes, extremely different approaches to a problem can lead to an identical (or very similar) solution. This is another way of saying "there is more than one way to give a cat a skin".
- An unorthodox method can be validated by one who is orthodox. This is what we will do today.
I hope I have made it clear to my readers that my models are being processed. I think the job is promising, I use it myself to make decisions. But, I am constantly taking advantage of this puzzle that we call Bitcoin, constantly learning new things and perfecting my approach. So, as I said before, make sure you take information from multiple high quality sources and see what makes sense to you.
Fortunately, I think that what you will see today gives further credibility to my pricing models, which were a completely new approach that I have experienced.
My work so far
Since I started publishing on Seeking Alpha, I have introduced many Bitcoin pricing models. I also published how the data were obtained, how to replicate my results and from time to time I made improvements to existing processes. If you wish to review this work, you can do it below.
Today we will take a step back and add another level of validation to the idea that the price of Bitcoin should not be considered in isolation. I argue that the price of Bitcoin is closely related to the fundamentals of the underlying network. Let's recap:
- Bitcoin is a currency that is also a network. Just like other social networks, value is in the community.
- Without community, the price is low. With a large and active community, the price is high.
- The total number of transactions is a way to quantify the age of Bitcoin. If he stops becoming "older", he is dead. If it continues to grow, the experiment continues.
- We can address the number of users using unique addresses. This is not perfect but it is powerful.
- We can perform proxy tasks using the number of daily transactions.
- The hash power of the miner is related to price, but also affects the security of the network and companies that invest hundreds of millions of dollars to control even 1% of the network hash rate.
Not-a-pear-what-now?
Non-parametric statistics are a collection of statistical approaches and models that can be applied to some data to verify or refute a hypothesis. According to Investopedia:
Non-parametric statistics refer to a statistical method in which data are not required to adapt to a normal distribution. Nonparametric statistics use data that is often ordinal, which means that it is not based on numbers, but rather a ranking or order of sorts. For example, a survey that broadcasts consumer preferences ranging from pleasure to love would be treated as ordinal data. – Investopedia.com
Since the price of Bitcoin is generally the subject of my studies, and that the price changes with the passage of time, they are considered time series data, which are not normally distributed.
So, today we will examine some ranking data and apply an approach called Spearman & # 39; s Rho to see if the underlying assumptions we have made can be verified.
By this I mean the price of Bitcoin regardless of the hash rate, total transactions, unique addresses and daily transactions? Let's say that our null hypothesis is this:
H0: There there is no relationship between the price of Bitcoin and the hash rate, the number of daily transactions, the total number of transactions and the number of unique addresses in use.
H1: There it's a relationship between the Bitcoin price and the data described above (hash rate, transactions, etc.).
We must either refute the hypothesis null, or we must accept it. In this case, denying the hypothesis does not mean accepting H1; that there is a relationship of some kind. Let's begin.
Ranking
The first thing we need to do is take our data and apply ranks to the values that Excel can do very quickly.
The way the rankings work is that the highest value will get the rank of "1", and at each value that is lower it is assigned a number that refers to its position in the stack. So, if we had 1533 data points (which we do) the lower Bitcoin price would give a rank of "1533". Let's start with the price, then:
- Low price (eg $ 0.06) = High rank (1533)
- High price (for example $ 20k) = Low grade (1)
We do the same for each of our other data sets and end up with something that looks like this spreadsheet below.
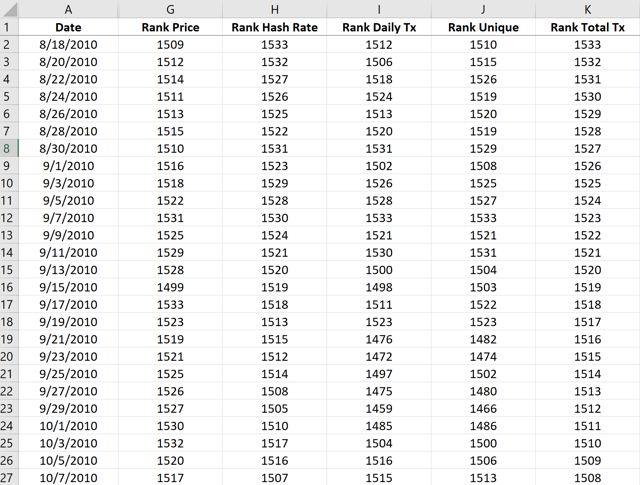 Source: blockchain.com and e-reader of the author
Source: blockchain.com and e-reader of the author
Now that we've done all that hard work, we do a visual check and see if these rankings tend to move together before doing more math.
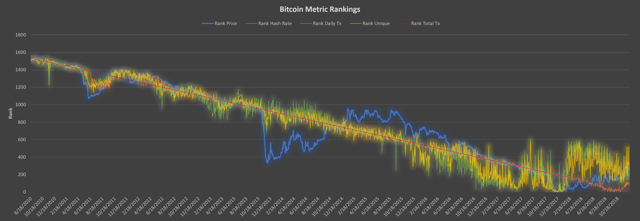 Source: blockchain.com and graphics of the author
Source: blockchain.com and graphics of the author
What you are looking at is simply the ranking of each category on a line chart. The Y axis is the ranking and the X axis is the time. As we can see, rankings tend to decrease over time, indicating that most of the lower values have occurred in the past (higher numerical rankings) and that higher values tend to be more recent.
This visualization seems to contradict our null hypothesis. To confirm that our eyes are not deceiving us, we run Spearman's Rho and see what it is.
To do this, we simply solve a correlation coefficient on the ranking data of each series. This was the result.
| Data pair | Correlation coefficient | P-value |
| Price: hash rate | , 938.386361 millions | 0 |
| Price: Daily transactions | , 885.603855 millions | 0 |
| Price: unique addresses | , 917.587142 millions | 0 |
| Price: Total transactions | , 935.037999 millions | 0 |
Source: author's e-mail sheet (data from blockchain.com)
The results indicate that indeed c & # 39; and & # 39;s a relationship between the rankings of these data sets. The direction of association is positive for all groups and each P value is well below the threshold for statistical significance.
Therefore, we must reject the null hypothesis.
What does all this mean?
It means that the price of Bitcoin is not an independent and unknowable phenomenon. The price of Bitcoin is only part of the Bitcoin ecosystem, and appears to be highly volatile. We can use it to our advantage if we know the nature of the beast. Fortunately for us, all data is in the open, if we know what to do with it.
Investing in Bitcoin can be a dangerous game, but if you get into the knowledge of how the system works, how it grows and you know what the failure looks like, then you'll be far ahead of the curve. By the way, if you are following someone in the cryptographic space and can not define a failure or admit that it is possible, you are following the wrong person.
Greetings,
Hans
This article was first published in Crypto Blue Chips.
Revelation: I am / we are long BTC-USD. I wrote this article alone, and expresses my opinions. I'm not getting any compensation for this (other than Seeking Alpha). I have no business relationship with any company whose actions are mentioned in this article.
[ad_2]Source link