What is the problem of the Byzantine generals and how does Blockchain solve it?

Anyone interested in cryptography, at some point has heard of the problem of "Byzantine generals". This problem has been the main stepping-stone for any secure and decentralized voting system created in the past. Originally written in an article created by Leslie Lamport, Marshal Pease and Robert Shostak, he describes a situation in which different parties involved need to vote and create consensus on their future actions. The problematic part is the possible existence of rogue and malicious members who could vote in a way that could make the whole system fail.

The problem can be practically described with three imaginary Byzantine generals preparing to attack or withdraw from a siege (an example with three generals is the easiest to understand). Every general has his own army, and these armies are positioned on various sides of the besieged city. The city is strong enough to handle a single army attacking it, perhaps even two of them at the same time; he will bend if he has to defend himself against all of them. The generals need to communicate with each other and make sure their armies attack simultaneously, as this is the only way the city can be taken. Each general will send a message to the other two, saying if and when he wants to attack. They can reach a consensus on the execution of an attack (if two thirds are agreed on an exact date) or they can also decide that the city can not be taken at this time and withdraw.

Only one army that attacks by itself is destined to fail

Communication is managed with the help of messengers. These messengers will run through the enemy city, exposing themselves to danger, and will try to hand over their message to the generals of other armies. General 1 could inspect the city and with the help of his military tactics he decides, for example, to attack on the following Tuesday evening. Then he will send a messenger to two other generals and inform them of his desired attack date. Ideally, both generals will receive the same message to attack Tuesday evening. To further confirm the attack plans, General 2 could agree on General 1's plan and send messengers to signal his willingness to attack Tuesday night. His messenger, ideally, will reach the other unharmed generals and deliver his message. In this way, the decision on when to attack was confirmed; The attack can start as soon as the sun sets on Tuesday.

However, every time a messenger is directed towards a general, he risks being discovered by the defenders of the city. If the messenger is captured, the defenders will know what the plan of one of the armies is. Naturally, the defenders will want to avoid a coordinated attack so that they can replace the original messenger with one of their own people. This messenger could then deliver a false message to one of the generals; this message could suggest a withdrawal or an attack on a different date, which would endanger the whole operation. Moreover, the original messenger himself could see the suffering that the besieged city is undergoing and decides instead to work in their interest. In the end, one of the generals might have problems with one of the other two generals; this complaint could cause him to become evil against the general he does not like. In his malice, he could send a message of withdrawal to the general he likes and a message of attack to the general he does not like, making the army of the despised general die in battle.

If one of these scenarios takes place, a traitor becomes active within the system; as a result, a communication error will occur and consent will not be reached. It is likely that one of the generals will make a wrong decision and condemn his men to a death on the battlefield.

The problem here is the lack of ability to check if the message is authentic or not. The generals must believe that their message has been correctly delivered to the other armies. Even if the messengers are captured, the message must be encrypted in some way to ensure that the city's defenders do not implement the attack strategy or that the malicious generals do not lead the entire army to the massacre. This problem of creating an untrustworthy system that allows "good guys" to communicate without revealing their plans to malicious players is the so-called Byzantine problem.

How Bitcoin Blockchain solves this problem

With Bitcoin, the problem of the Byzantine generals turns into an even more complicated beast. The number of generals increases and now each of them must communicate their intentions to all the other generals safely and quickly. At the same time, the number of evil players and possible traitors increases, which means that each of them must be neutralized in some way.

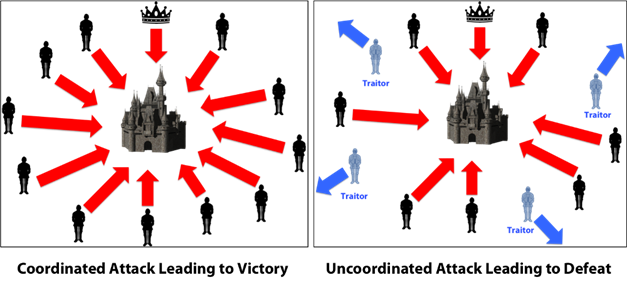
Source: https://medium.com/@DebrajG/how-the-byzantine-general-sacked-the-castle-a-look-into-blockchain-370fe637502c

Using blockchain technology, the problem of the Byzantines can be solved. A distributed digital ledger operating on a computer network has millions of members / generals who are not under any hierarchy but who are actually considered equal. Each member of the network must vote on which message the network should agree.

Blockchain offers a decentralized and autonomous way of managing this network of users. Each blockchain contains data on all previously conducted and recorded transactions. The blockchain is constantly updated with new data and new transactions, tracking every single token that has ever been created or spent on the network. The creators of Bitcoin have made sure that these blockchain data were tamper-proof using special cryptographic solutions based on the SHA256 hash algorithm.

Bitcoin's cryptography solution addresses this problem by adding a nonce (a string of unique numbers and letters to your communication) to your text message and then inserting it into the SHA256 hash algorithm. This nonce is a key element of this system security; when passing through the SHA256 hash algorithm alongside the message, if it has been sent from a trusted source, it will provide a hash that starts with a certain number of zeros.

Now, to apply this to our generals, every general must agree on a single message. Every general can not trust any other general on the network. Every general can not trust the communication channel itself (the city through which the messenger passes); they must assume that the message can be intercepted and replaced with false data. This would result in loss of value and the creation of an unstable network. Therefore the sending of a pure text message is out of the question.

First, the general who sends the message finds a nonce (usually takes millions, even billions of attempts) which, once passed through the hash algorithm, will give a hash function that starts with a number of zeros set to. The message is then sent to the general with the nonce. The receiving general then blocks the message + nonce through the same hashing algorithm. If the resulting hash has the same number of zeros that had the initial hash, then the general can be sure that the message was sent by you. If the number of zeros is less than the original hash, it has probably been intercepted and certainly tampered with.

There is still a way for the city to create a fake message. If they replace the message itself, the hash function will not start with the same number of zeros. Now the city will have to spend billions of attempts to find a nonce that, when executed through a hashing algorithm along with the false message, creates a hash function that will have the same number of zeros as the original.

This problem is solved by making the number of attempts necessary to find the hash beginning with a number of zeroes that is practically impossible to execute. Since we have more generals, each of them will have their message related to the day of the attack. To deceive the city, more generals will add their message in a single block and collectively seek to find a nonce such that the hash of the messages and said nonce will start with a certain number of zeros (the more zeros, the harder it will be to find the nonce). All generals will need to use a lot of computational power and energy to find this nonce. When it has been found, the message + nonce is finally sent.

As can be deduced from here, the city will have a very difficult period with the modification of the contents of the message even if they capture the messenger. With more messages and more generals investing a lot of computational power, it is virtually impossible for the city to tamper with the message.

And that's how it works. To make it parallel to the same Bitcoin network, people who want to make transactions on the network protect their transactions by protecting them against hash and nonces algorithms powered by a network of powerful mining nodes (which basically uncover block blocks and add blocks to the blockchain). A network user who wants to tamper with the blockchain simply can not compete with the entire Bitcoin ecosystem, making transactions safe and tamper-proof.

This article was inspired by a great one video produced by Ivan on Tech, which you should definitely see for further details and illustrations. You can also check this time presentation by Andreas Antonopoulos who goes deeper even further to explain this problem.